小朋友都喜欢看魔术，如果能自己表演几个小魔术，那就更酷了，可以收获很多同伴的崇拜哦！今天小编给大家盘点一下，有哪些道具简单、一学就会的数学小魔术。

猜数

拿出五张卡片，分别写满很多数字，像下图一样。想偷懒的家长，自己下载后打出来就能用了。

玩法很简单，先找一位观众，写一个1~31之间的数字，不要让魔术师看到；然后魔术师向他出示这五张卡片，让这位观众指出，他写的那个数字都在哪几张卡片上。

观众指出后，魔术师立马就能告诉大家：这个观众写的数字是几，是不是很神奇！

魔术揭秘

这个魔术利用的是二进制原理——逢二进一。

这五张牌的第一个数分别对应2的0次方、2的1次方、2的2次方、2的3次方、2的4次方，也就是二进制中的1、10、100、1000、10000。

每张表中的数字都有一个特点，即：将这个数字写成2的多项式后，必含有第一个数字。比如，第五张牌的27可以写成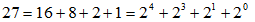
因此，27出现在16开头的第五张牌中，也出现在8开头的第四张牌、2开头的第二张牌和1开头的第一张牌中，但没有出现在第三张牌中。

猜扑克牌

一共27张扑克牌，观众任选一张，不要告诉魔术师。

魔术师把27张牌按1、2、3、1、2、3……的顺序分成三排，每排9张，然后让观众指出他挑选的牌在哪一排。

接下来，魔术师先把观众挑选的这一排按顺序收起来，然后依次收另外两排。

全部收好后，魔术师再次把这27张牌按1、2、3、1、2、3……的顺序分成三排，每排9张，让观众指出他挑选的牌在哪一排。

这样重复三次，魔术师收好牌后，把最上面的那张交给观众，真是神奇了，恰好就是观众想的那张牌！

魔术揭秘

这仍然是利用进制变花样，只不过这次不是二进制，而是三进制。

其实道理很简单，第一次收牌后，那张秘密牌处于前9张牌中，可当你把它们又平均分成三排之后，这9张牌也被分到三个不同的排中，并且都在各自的排名列前三。当你再次收牌时，那张秘密牌现在就处于所有牌的前三名了。接下来，这三张再次被平均分成三排，并且都是“排头兵”。观众再次选择时，这张牌终于跑到了第一的位置上。

斐波那契之谜

斐波那契数列大家都听说过，如果一对公母兔子从生下来到第三个月初便能生一对公母兔子，并且以后每个月生一对的话，那从年初你有一对兔子，到接下来的12个月，你将依次会有：1、1、2、3、5、8、13、21、34、55、89、144对兔子。

这个数列的规律就是：从第三项开始，每项都是前两项的和。

请观众任意写下两个数，从第三个数开始，每个数都是前两个数的和。你只需要把你的第十个数是几告诉我，我就能推出你写的两个数是哪两个数。

魔术揭秘

如果我们把第一个数当成X，第二个数当成Y的话，那么到了第十个数，就应该是（21X+34Y），而第九个数，应该是（13X+21Y）。

拿第九个数去除第十个数，虽然中间有两个未知数，但由于13：21=0.619，而21：34=0.6176两个数都非常接近我们的黄金分割点0.618，所以这个比值会非常接近0.618，跟X、Y的具体值关系不大。

这样，我们就可以通过第十个数×0.618，再取整得到第九个数，有了第九个数，剩下的倒推就可以了。

例如：第十个数是123，123×0.618=76.014≈76，则第八个数应该是123－76=47，第七个数应该是76－47=29……依此类推，直到求出前两个数分别是1、3。

预言牌

首先要有一幅牌，洗过之后（谁洗都行），魔术师装作手放到牌上“感应”，然后在纸上写下一个牌点（比如：红桃7）。

接下来，要求观众在10~19中间说一个数，比如15，数出前15张牌。然后，让观众把他的两位数的两个数字相加，1+5=6。请观众从后往前数出第六张牌。

魔术师把自己事先写好的纸片翻开，天呐！观众手里拿的那张牌，恰好就是他纸上写的，红桃7。

魔术揭秘

其实这个魔术对于成年人来说要想揭穿它，一点都不难。不管观众选的是十几，当他把这两个数字相加，并从后往前数到这一张时，他挑的必须是整幅牌的第十张，魔术师只需要偷偷地看下第十张牌，并抄下来就行。

磁性表演

磁性表演

在桂林起伏秀丽的山峦里，蕴藏着曲折离奇的洞穴。七星岩有个可容纳万人的大洞，狭窄的孔道，连着宽敞的“大厅”。

在数字王国，你也能看到一些奇穴怪洞。这里介绍的是一个具有魔力的磁性黑洞，它的魔力像是磁性吸力一样，把好多好多数字都能吸进洞里。

数字1089就是一个很大很大的磁性黑洞。

你只要任意找一个三位数，要求三个数位上的数各不相同，数的末尾不是0，例如：623。我们先把623这个数的各位数字颠倒一下，得到326，然后用623-326，它们的差是297。

再把297各位数字颠倒过来，得792，然后用297+792，它们的和是1089。

这样，原来的数623就被吸到1089“黑洞”里去了。

我们再举几个例子。如

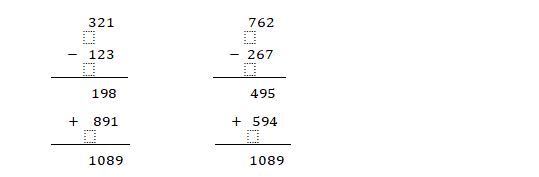
同样，321、762等都被变成了1089。

如果三位数中首位数较小，颠倒后，用大的数去减原来的数。例如489，三位数字颠倒后变成984，那么，就用984-489=495，再用495+594=1089。

1089这个磁性黑洞，一般只对三位数有吸力，而且如果各位数字都相同，如111、222等，它的磁力就不起作用了，因此，如果要侦破这个洞的秘密，可以用相同数字的三位数去当“侦探”。

我们细心地分析一下，就会发现1089黑洞有一个特定的规律，就是当你在进行计算时，如果遇到三位数中首位和末位（百位和个位）数字之和正好等于中间一位数（十位），且是“9”时，那么这两个数的和就一定是1089。而一个三位数数字，首位和末位数字交换后，得到的两个数之差必定会出现上面的现象，即首位加末位等于中间数“9”。

例如：478这个数，把4、8交换位置后，得到874，用874-478=396,“396”这个数的“首位”3加上末位“6”，正好等于“9”。那么，这个数字再变成693时，396+693就必然等于1089。这就是1089黑洞的奥妙之处。

所以，如果我们用一个各位数字都相同的数去计算时，就不会出现“1089”黑洞了。

在数字中，还有一个比1089更大的磁性黑洞就是6174，它专门吸进四位数字，当然也是四个数字各不相同的。

例如：7380，我们先将7、3、80从大到小组成一个新数8730,再按从小到大组成另一个新数0378，然后求它们的差。

再对8352重复进行如上所述的计算。

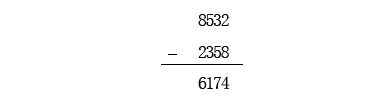
这样，原来的7380这个数就被吸进6174这个神奇的黑洞里去了。

我们再换几个数试一试。

例 (1) ：3654 例（2）：7126

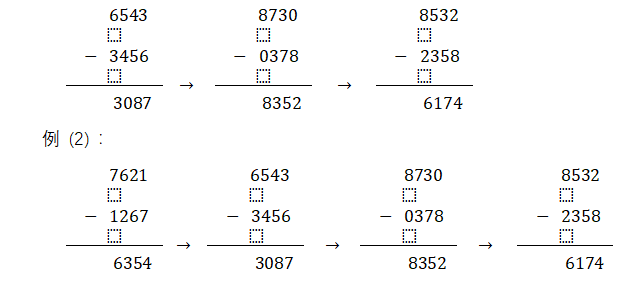
这下你信服了吧！3654、7126又被吸进6174的黑洞里去了。

聪明的读者，你可能已经发现了“6174”黑洞的奥秘了。如果还没有发现的话，我提醒你注意一下，你可曾看到刚才三个例子中，当算到最后一个算式时，得到的四位数是“8532”。“8532”这个数就是“魔”数了。当出现“8532”时，用8532-2358

就必定等于“6174”了。当然，如果最后结果不直接是8532，也可能是其他的数，也能转.进黑洞去的。例如：4728这个数。

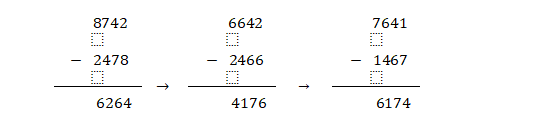
这个算式的最后一个数是“7641”，这也是“魔”数。

你有兴趣的话，还可以多找一些数字试试看，找找哪些数字最容易进黑洞，哪些数字最难进黑洞。

不过，还要提醒你，特殊的四位数，也就是四个数字相同的四位数：1111、2222、3333……是永远进不了黑洞的。

旋涡表演

漩涡表演

在数字海洋里，有一种堪称湍流激荡的漩涡，不知你是否见过？

我们只要把一个四位数的每一个数字都平方，然后相加，得到一个答案；然后再平方相加，这样继续下去，就会出现一个奇特的数字漩涡。例如，1986这个数，先把1、9、8、6平方，然后相加，得到：

这样不断地做下去，就得到一串长长的数字，很快就会发现这些数字像漩涡一样转了起来。

你看：

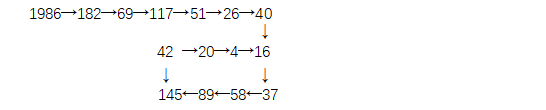
这就是“数字海洋”中遇到的“数字漩涡”。我们不妨再随便找一个数来试试。

如3875：

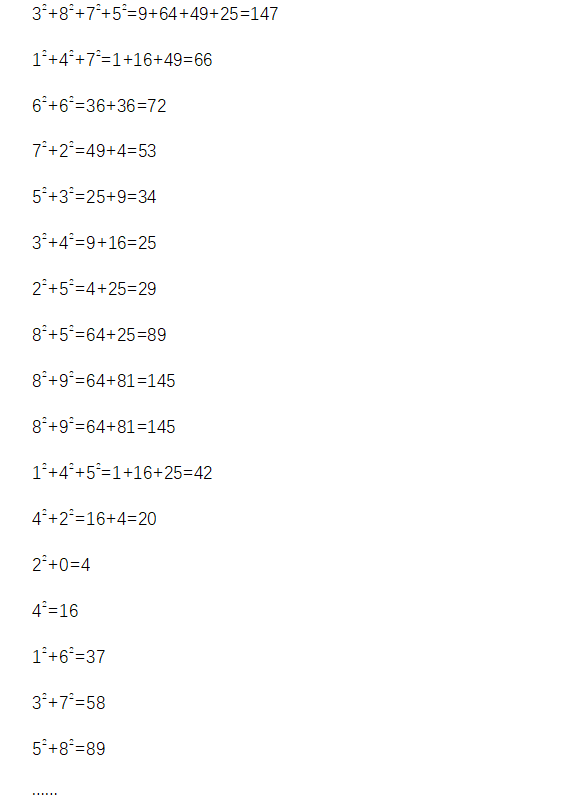
我们对这个数字算了这么多次，使这个数字形成了一个漩涡。如下所示：

从这个例子可以看出，尽管这个数字我们算了9次后，才出现漩涡现象，但毕竞又出现了漩涡。这样的奇迹总是会有的。不同的是：它们出现的时机不相同。

我们再来看一个特定的数，如7777。

我们先把7777的每一位数字平方，然后相加，得16，再依次类推，继续做下去，那么就又出现了下面这样奇特的漩涡。

在数字海洋中，这样的游涡几乎处处可见，我们再看下面两个例子。

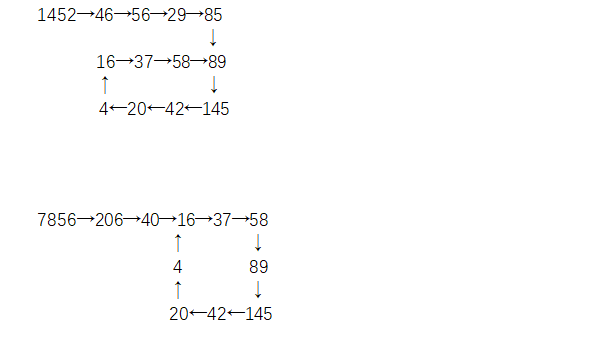
我们如果再做几个，或者几十个，可以从中发现一些规律，发现这些漩涡最容易从哪一些数字开始旋转。这也是一个十分有趣的学问。从刚才几个例子中，也许你已发现了当数字是16、58、89时，很容易产生漩涡。

为什么当数字是16、58、89时，容易出现漩涡呢？因为当数字是16、58、89时，会出现下列的情景。

如果有兴趣的话，还可以再试试，找找其中的奥妙。

在数学海洋中，“漩涡”是普遍存在的现象。只有少数一些数字例外。如1112：

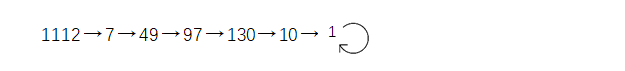
因为当算到结果是10时，再下一个得数是1，因为“1”的平方还是1，那就只能永远得1。如果把这种现象也算做漩涡的话，那就是一种原地打转的特殊漩涡了。